Is 5/8 Bigger Than 3/4
tresmisiones
Sep 24, 2025 · 6 min read
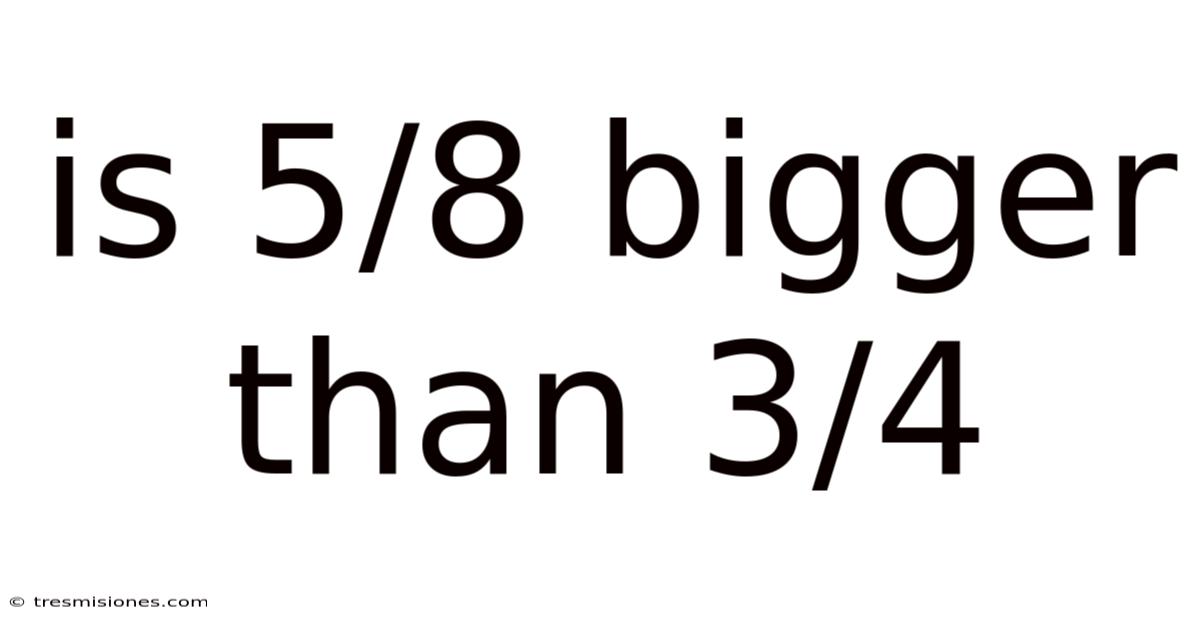
Table of Contents
Is 5/8 Bigger Than 3/4? A Deep Dive into Fraction Comparison
Determining whether 5/8 is bigger than 3/4 might seem like a simple task, especially for those comfortable with fractions. However, understanding the underlying principles behind fraction comparison is crucial for building a strong foundation in mathematics. This article will not only answer the question definitively but will also delve into multiple methods for comparing fractions, exploring the underlying mathematical concepts, and providing practical examples to solidify your understanding. We'll also address common misconceptions and frequently asked questions.
Introduction: Understanding Fractions
Before we compare 5/8 and 3/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator, representing 3 out of 4 equal parts.
Method 1: Finding a Common Denominator
This is arguably the most common and reliable method for comparing fractions. The key principle here is to rewrite the fractions so they share the same denominator. This allows for a direct comparison of the numerators.
-
Step 1: Find the Least Common Multiple (LCM) of the denominators. The denominators in our case are 8 and 4. The LCM of 8 and 4 is 8 (because 8 is a multiple of 4).
-
Step 2: Convert the fractions to equivalent fractions with the common denominator. We need to rewrite 3/4 with a denominator of 8. To do this, we multiply both the numerator and the denominator by 2: (3 x 2) / (4 x 2) = 6/8.
-
Step 3: Compare the numerators. Now we compare 5/8 and 6/8. Since 5 < 6, we conclude that 5/8 < 6/8. Therefore, 5/8 is smaller than 3/4.
Method 2: Converting to Decimals
Another effective method involves converting the fractions to their decimal equivalents. This method is particularly useful when dealing with more complex fractions or when you have a calculator handy.
-
Step 1: Divide the numerator by the denominator for each fraction. 5/8 = 0.625 and 3/4 = 0.75.
-
Step 2: Compare the decimal values. Since 0.625 < 0.75, we again conclude that 5/8 is smaller than 3/4.
Method 3: Visual Representation
Visualizing fractions can be a helpful approach, especially for beginners. Imagine a circle divided into sections.
-
Representing 3/4: Divide a circle into four equal parts and shade three of them. This visually represents 3/4.
-
Representing 5/8: Divide a separate circle into eight equal parts and shade five of them. This visually represents 5/8.
By comparing the shaded areas, it becomes clear that the shaded area representing 3/4 is larger than the shaded area representing 5/8. This visual confirmation reinforces the conclusion that 5/8 is smaller than 3/4.
Method 4: Cross-Multiplication
This method offers a more algebraic approach to comparing fractions.
-
Step 1: Cross-multiply the numerators and denominators. Multiply the numerator of the first fraction (5) by the denominator of the second fraction (4): 5 x 4 = 20. Then, multiply the numerator of the second fraction (3) by the denominator of the first fraction (8): 3 x 8 = 24.
-
Step 2: Compare the products. Since 20 < 24, the fraction that resulted in the smaller product (5/8) is the smaller fraction. Therefore, 5/8 is smaller than 3/4.
Why these methods work:
Each method relies on fundamental mathematical principles. Finding a common denominator ensures that we're comparing "apples to apples," working with equal-sized units. Converting to decimals provides a numerical representation that's easily comparable. Visual representation leverages spatial reasoning to intuitively grasp the relative sizes. Cross-multiplication is a shortcut based on the properties of proportions.
Addressing Common Misconceptions
A common mistake is to simply compare the numerators and denominators without finding a common denominator or converting to decimals. This approach is inaccurate because it doesn't account for the size of the units (the denominators). For instance, someone might incorrectly assume that 5/8 is larger than 3/4 because 5 > 3. This is a crucial point to understand: the denominator plays a vital role in determining the fraction's value.
Expanding the Understanding: Working with More Complex Fractions
The methods described above apply equally well to more complex fractions. For example, let's compare 7/12 and 2/3.
Using the common denominator method:
- The LCM of 12 and 3 is 12.
- 2/3 is equivalent to (2 x 4)/(3 x 4) = 8/12.
- Comparing 7/12 and 8/12, we see that 7/12 < 8/12, so 7/12 < 2/3.
Using the decimal method:
- 7/12 ≈ 0.583
- 2/3 ≈ 0.667
- Again, 7/12 < 2/3.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to compare fractions? A: Yes, you can use a calculator to convert fractions to decimals, making the comparison straightforward.
-
Q: Is there a single "best" method for comparing fractions? A: The best method depends on your comfort level and the specific fractions involved. Finding a common denominator is generally reliable, while converting to decimals is quick and efficient with a calculator. Visual representation is excellent for building intuition.
-
Q: What if the fractions have very large numbers? A: Even with large numbers, the methods described above still apply. Using a calculator to find the LCM or to convert to decimals will be particularly helpful in such cases. You might also consider simplifying the fractions before comparison to make the process easier.
-
Q: Why is understanding fraction comparison important? A: Fraction comparison is a foundational skill in mathematics. It's essential for solving equations, understanding proportions, and working with various mathematical concepts in algebra, geometry, and beyond.
Conclusion: Mastering Fraction Comparison
This article has provided a comprehensive exploration of how to compare fractions, specifically addressing the question of whether 5/8 is bigger than 3/4 (it's not). We've explored multiple methods, highlighted common pitfalls, and expanded on the application of these techniques to more complex scenarios. Mastering fraction comparison isn't just about getting the right answer; it's about understanding the underlying mathematical principles and developing a strong foundation for future mathematical endeavors. Remember to practice regularly to solidify your understanding and build confidence in tackling various fraction-related problems. By employing the methods described, you can confidently compare any two fractions and accurately determine which is greater.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 5/8 Bigger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.